本文主要针对PPO[1]算法的目标函数谈一点自己的理解,刚刚入门的小白,文中不对之处还望各位大佬批评指正。
PPO主要针对TRPO[2]算法进行了改进,在保证具有TRPO算法性能的基础上,PPO实现更加简单,更具有通用性,同时有着更好的采样复杂度。
Trust Region Methods
策略梯度的目标函数为:
$$
L^{PG}(\theta) = \hat{E}t [log ;\pi{\theta}(a_t | s_t)\hat{A_t}]\tag{1}
$$
置信域方法的目标函数为:
$$
\begin{aligned}
\underset{\theta} {maximize} \quad \hat{E}t[\frac{\pi_\theta(a_t|s_t)}{\pi{\theta_{old} }(a_t|s_t)}\hat{A_t}] \\
subject; to \quad \hat{E}t\bigg[KL[\pi{\theta_{old} }(\cdot |s_t),\pi_\theta(\cdot |s_t)]\bigg]
\end{aligned}\tag{2}
$$
根据(2)式可见置信域方法在策略梯度的基础上增加了约束,限制前后两个策略差异不大,而KL散度是衡量两个策略差异的。置信域方法解决了参数更新过快导致的难以收敛的问题。
之后提出的TRPO改进方法,将(2)式转换为了一个无约束的优化问题:
$$
\underset{\theta} {maximize} \quad \hat{E}t\bigg[\frac{\pi_\theta(a_t|s_t)} {\pi{\theta_{old} }(a_t|s_t)}\hat{A_t}-\beta KL[\pi_{\theta_{old} }(\cdot |s_t),\pi_\theta(\cdot |s_t)]\bigg]\tag{3}
$$
但系数 $\beta$ 的选择是一个比较困难的问题,直接选用一个固定的参数进行SGD更新的效果并不会很好。
Clipped Surrogate Objective
对于(2)式,如果令$r_t(\theta)=\frac{\pi_\theta(a_t |s_t)}{\pi_{\theta_{old}}}$ ,那么即可得到:
$$
\begin{eqnarray}L^{CPI}(\theta)=\hat{E}t\bigg[\frac{\pi_\theta(a_t|s_t)} {\pi{\theta_{old} }(a_t|s_t)} \hat{A_t}\bigg] = \hat{E}_t\bigg[ r_t(\theta)\hat{A_t}\bigg]\end{eqnarray}\tag{4}
$$
如果对(4)式求最大值,会导致前后两个策略差异过大,也就是会导致$r_t(\theta)$过于偏离1, 影响性能,那么需要对(4)式进行修改,限制策略差异大小,即对$r_t(\theta)$设置一个范围
$$
\begin{eqnarray}L^{CPIP}(\theta)=\hat{E}_t\bigg[min( r_t(\theta)\hat{A_t},clip(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A_t})\bigg]\end{eqnarray}\tag{5}
$$
其中$clip(x,up,down)$表示将x限制范围$[up,down]$ ,那么(5)式就将$r_t(\theta)$限制在$(1-\epsilon,1+\epsilon)$之间,一般取$\epsilon = 0.2$,(5)式也就是PPO的目标函数,论文中对于(5)式进行了绘图表示。
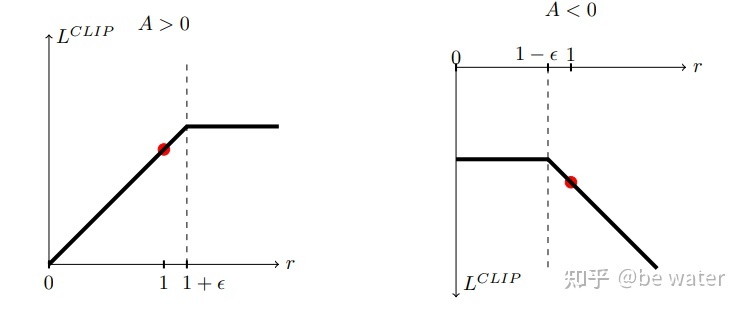
通过图1,并结合(5)式,那么可以将(5)式修改为:
$$
\begin{eqnarray}
\begin{aligned}
if \quad &\hat{A_t}>0\quad
L^{CLIP}(\theta)=\begin{cases} (1+\epsilon) \hat{A_t} \quad &r_t(\theta)>1+\epsilon \\
L^{CPI}=r_t(\theta) \hat{A_t} \quad &else\end{cases}\\
if \quad &\hat{A_t}<0 \quad
L^{CLIP}(\theta)=\begin{cases} (1-\epsilon)\hat{A_t}\quad &r_t(\theta)<1-\epsilon \\
L^{CPI}=r_t(\theta) \hat{A_t} \quad &else\end{cases}
\end{aligned}\end{eqnarray}\tag{6}
$$
$\hat{A_t}$代表t时刻的优势函数,$\hat{A_t}$大于0表示此时策略更好,要加大优化力度。目标函数$L^{CLIP}(\theta)$取最大,那么就会尽量取大的$r_t(\theta)$。但如果更新力度过大,新旧策略差异太大,即$r_t>1+\epsilon$,显然这不是我们希望的,那么clip操作和min操作会选择$r_t=1+\epsilon$,这样就将最大的$r_t$限制到了$1+\epsilon$,防止了过度优化。
同样$\hat{A_t}$小于0表示此时策略更差,要减小优化力度,目标函数$L^{CLIP}(\theta)$取最大,那么就会尽量取小的$r_t(\theta)$。但如果更新力度过大,新旧策略差异太大,即$r_t<1-\epsilon$,显然这不是我们希望的,那么clip操作和min操作会选择$r_t=1-\epsilon$,这样就将最大的$r_t$限制到了$1-\epsilon$,减小了更新力度。
通过以上解释,对比TRPO的目标函数(式(2,3))和PPO的目标函数(式(5)),可以看到PPO的目标函数在限制前后策略差异不大的同时,避免了超参数的$\beta$调整的难度。仅从目标函数,就可以看到PPO算法在保障TRPO算法性能的同时,实现上更加简单。
参考
- ^John Schulman et al, Proximal Policy Optimization Algorithms: https://arxiv.org/abs/1707.06347
- ^John Schulman et al , Trust Region Policy Optimization: https://arxiv.org/abs/1502.05477

