图解NatureDQN和Double DQN

发布日期: 2022-03-02

学习强化学习的过程中，作为渣渣的我觉得入门很难。尤其是算法实现并不像深度神经网络那样逻辑清晰且框架成熟。看了网上DQN的很多讲解只是觉得理解了主要原理，对于实现还是无从下手，在看过相关代码才有了思路。因此作为渣渣的我决定把自己对于相关算法的理解绘制成图记录下来，方便刚入门的小白学习。当然本人能力有限，难免有所错误，欢迎大佬们批评指正。

部分符号说明

done：本轮游戏是否结束

$\phi(s)$ : 表示状态s的特征，在本文中与s代表意义基本一致。

$s 、 s_t$:本文中均表示当前状态

s’、$s_{t+1}$:本文中均表示下一状态

a、 $a_t$ :本文中均表示当前状态选择的动作

a’、 $a_{t+1}$ :本文中均表示下一状态选择的动作

Q、PolicyNet：均表示策略网络

$\hat{Q}$ 、TargetNet：均表示目标网络

$\theta$ 表示策略网络的参数， $\theta^-$表示目标网络的参数

方块表示标量，长条直角矩形表示向量，直角矩形表示表示矩阵。

需要注意的事，图中s和s’虽然用的方块，但其一般是向量或者矩阵，本文为了美观和与a、r、done的统一也表示成了方块。

Nature DQN

首先放出DQN2015[1]的伪代码

代码实现可以参考Datawhale EasyRL[2]的实现，本文的图也是在理解了其相关教程[3]和代码的基础上做的。

核心思想就是利用两个Q网络拟合Q-learning中的Q表，解决Q表难以处理连续状态的问题。难点就在于Q网络的参数更新，解决了Q网络的参数更新，就可以把Q网络看作Q表。

与环境交互部分

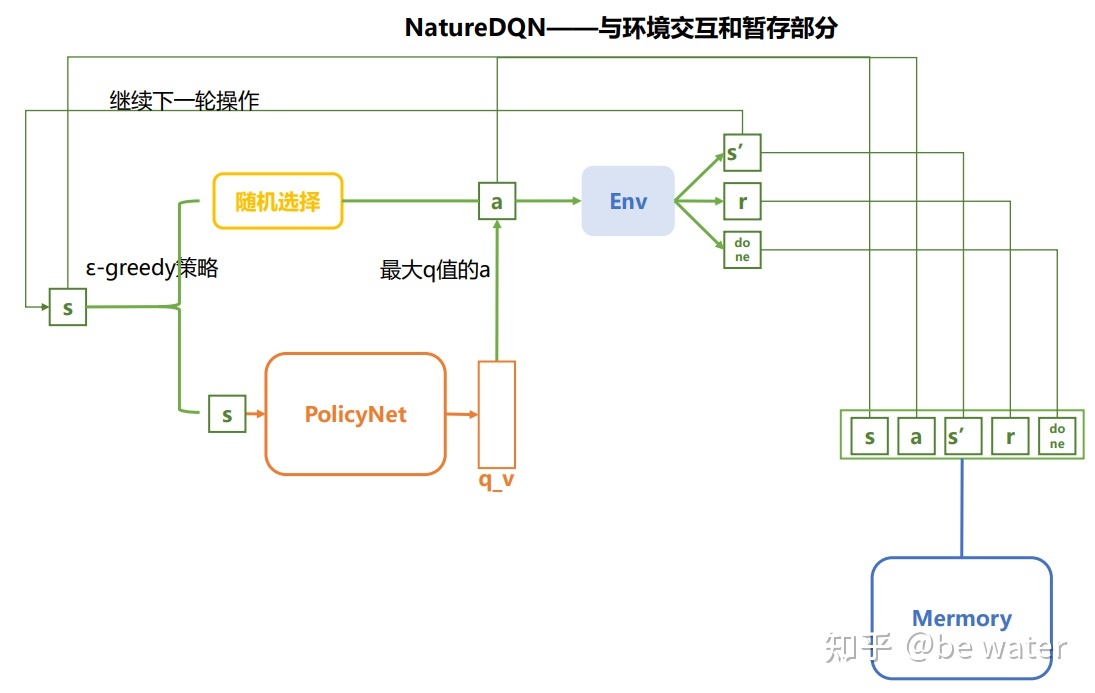PolicyNet对应于图1中的Q

以下对图2进行解释：

输入状态s（注：s一般为向量或者矩阵，即$\phi(s)$) ，表示对于状态s的特征提取**）后，算法根据$\epsilon-greedy$ 策略选择动作a；
将s、a输入环境，得到下一步状态s’ 、奖励r 、是否结束标志done；
将$<s,a,s’,r,done>$存储到回放区Mermory中。
更新状态s。

ε-greedy策略**[4]

$\epsilon-greedy$策略即有$\epsilon$的概率采取随机策略，$1-\epsilon$ 概率选择贪婪策略，公式如下：
$$
\pi(a|s) = \begin{cases} \epsilon/m + 1-\epsilon \qquad if ; a^* = argmax_{a\in A} Q(s,a)\\ \epsilon/m \qquad otherwise \end{cases}\tag{1}
$$

其中 m为动作个数，推导过程如下：

如果采用随机策略，那么
$$
\pi_{rand}(a|s) = 1/m\tag{2}
$$

如果采用贪婪策略，那么
$$
\pi_{greedy}(a|s) = \begin{cases} 1 \qquad if ; a^* = argmax_{a\in A} Q(s,a)\\ 0 \qquad otherwise \end{cases}\tag{3}
$$

那么$\epsilon-greedy$策略为：
$$
\pi(a|s) = (1-\epsilon)\cdot \pi_{greedy}(a|s) +\epsilon\cdot \pi_{rand}(a|s)\tag{4}
$$

将式（2）（3）代入式（4）即可得到式（1）。

具体实现：即给定一个随机数rand，如果随机数大于$\epsilon$,那么动作使用PolicyNet得到的q_v中的最大值对应的动作a，如果随机数小于 $\epsilon$,那么随机选择动作a。一般 $\epsilon$ 在训练过程中逐渐下降，即开始侧重于探索，最后侧重于利用。

从这里你也可以看出DQN算法适用于连续状态、离散动作的情况。

网络更新部分

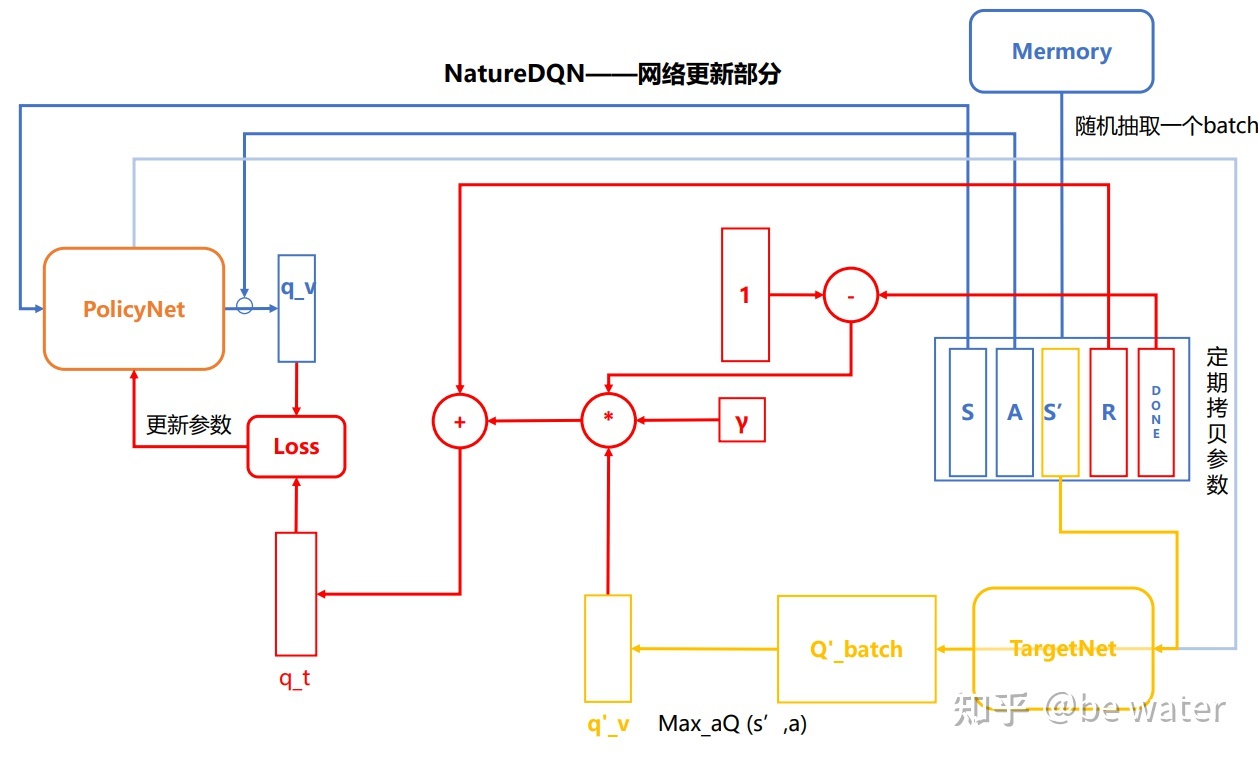
从回放区Mermory中随机抽取一个batch的$<S,A,S’,R,DONE>$；
将S、A给到PolicyNet，得到对应的估计Q值q_v。注意，只有S作为PolicyNet的输入，而A的作用在于在Policy的输出中找到对应A的q_v。步骤1、2对应图中蓝色的部分；
将S’给到TargetNet网络，得到Q_n_batch，对于每一个$s’\in S’$ ,在对应中的Q_n_batch中寻找最大的值，从而得到q_nv，即公式$max_{a’} \hat{Q}(\phi_{j+1},a’;\theta^-)$的实现。这部分对应图中黄色部分。
接下来是公式(5)的实现\

$$
y_j = \begin{cases} r_j \qquad if ; episode; terminates\\ r_j+\gamma max_{a’} \hat{Q}(\phi_{j+1},a’;\theta)\qquad otherwise\end{cases}\tag{5}
$$

EasyRL用式（6）代替(5)式，实现上更加简单。
$$
y_j = r_j+\gamma max_{a’} \hat{Q}(\phi_{j+1},a’;\theta)(1-done)\tag{6}
$$

这部分的实现也就是红色的部分（不包括Loss），最终得到目标Q值q_t（ $y_j$ ）.

\5. 最后就是熟悉的计算Loss环节，利用反向传播对PolicyNet的参数进行更新。那么TargetNet的参数什么时候更新呢，当PolicyNet更新n次后将其参数直接拷贝到TargetNet中，n是我们设置的参数。这样就要求TargetNet与PolicyNet的结构完全一致。

整体架构

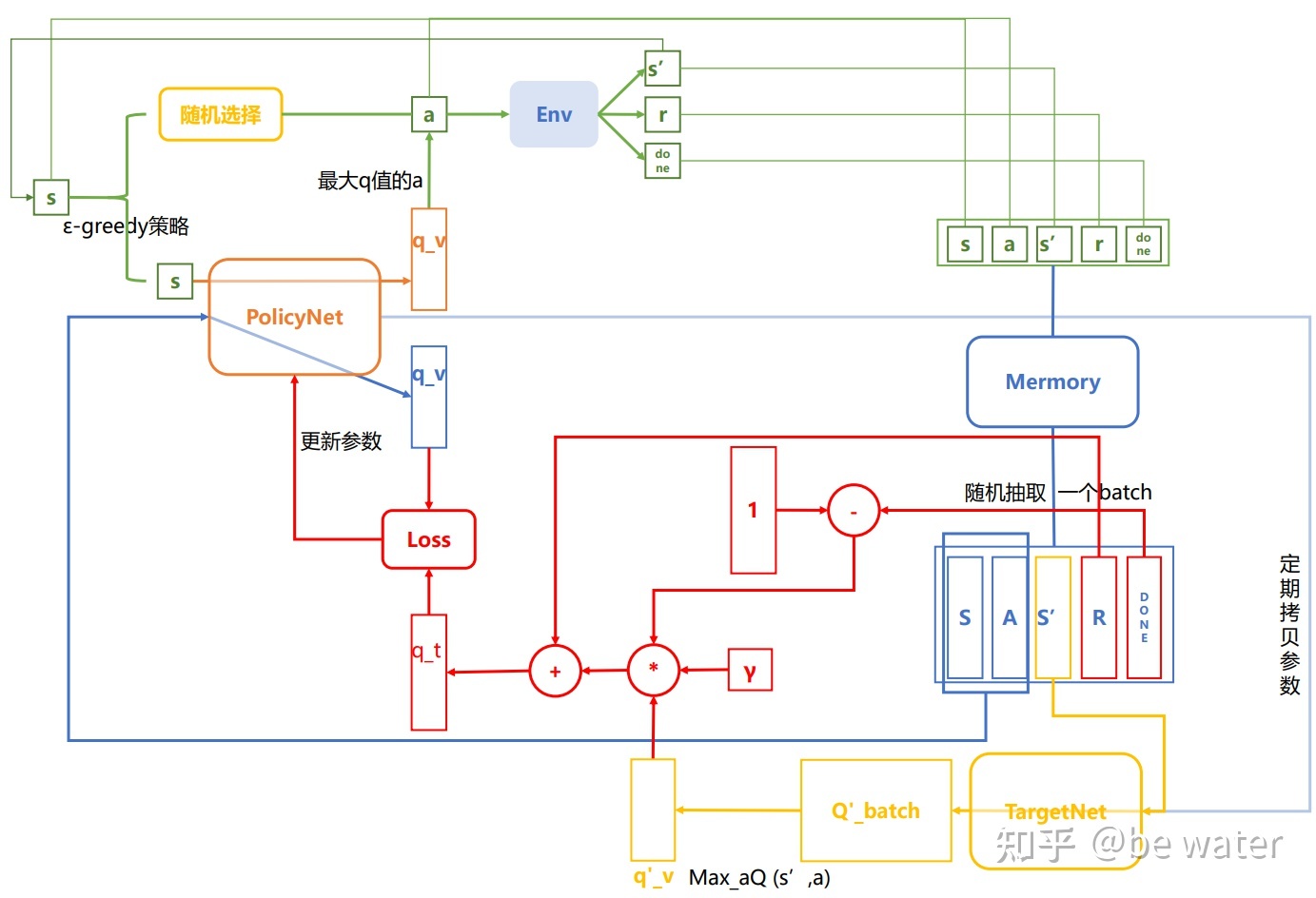图4

将图2和图3结合就得到了图4，为了美观，部分线条做了简化。图3呈现了完整的NatureDQN的训练流程。

Double DQN

Double DQN[5]与Nature DQN的区别就一个公式：
$$
y_t^{DQN} \equiv R_{t+1} + \gamma max_a \hat{Q}(s_{t+1},a;\theta_t^-)\\
y_t^{Double DQN} \equiv R_{t+1} + \gamma \hat{Q}(s_{t+1},argmax_a Q(s_{t+1},a;\theta_t);\theta_t^-)\
$$

Nature DQN对于状态$s_{t+1}$下的动作选择为，在TargetNet中的最大Q值对应的动作a，因此得到的Q值为$max_a \hat{Q}(s_{t+1},a;\theta_t^-)$；

DoubleDQN对于状态$s_{t+1}$下的动作选择为，在PolicyNet中最大Q值对应的动作a，因此得到的动作为 $a’=argmax_a \hat{Q}(s_{t+1},a;\theta_t)$，那么对应的Q值为：
$$
\hat{Q}(s_{t+1},a’;\theta_t^-)=\hat{Q}(s_{t+1},argmax_a \hat{Q}(s_{t+1},a;\theta_t);\theta_t^-)\tag{7}
$$

因此DoubleDQN的网络更新部分图如图5所示。

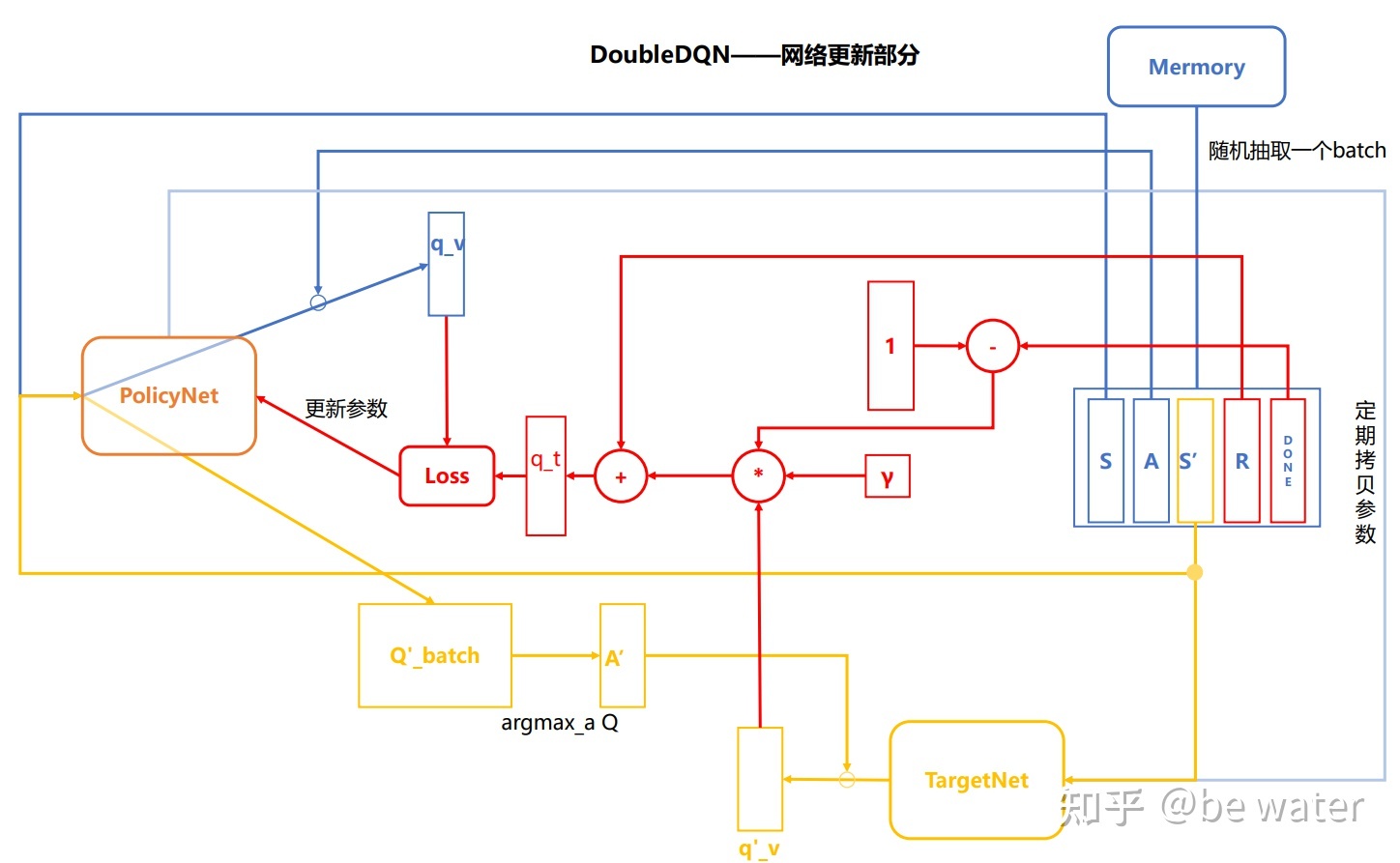图5